Unraveling The Riddle: What 'x*x*x Is Equal To 2024' Really Means
Have you ever stumbled upon a mathematical expression that makes you pause, perhaps a bit curious, or even a little perplexed? It's like finding a small puzzle in the middle of your day, you know? One such phrase that might catch your eye, especially as we move through this current year, is "x*x*x is equal to 2024." This seemingly simple statement, when you think about it, holds a fascinating mathematical concept at its core, something that many folks, from students to just general curious minds, often wonder about. It's a question that, in a way, touches upon fundamental ideas in algebra, inviting us to explore how numbers behave and what they can tell us.
For many, the idea of "x*x*x" immediately brings to mind something we call a cube, or a number multiplied by itself three times. It's a building block in mathematics, really, and solving for 'x' in this kind of equation means finding what's known as the cube root of 2024. This isn't just some abstract school problem, either; understanding these kinds of relationships is pretty useful. Just as people on platforms like Zhihu, a vibrant community for sharing knowledge, often look for clear answers to their questions, we're going to break down this particular numerical challenge.
So, what does it truly mean when we say "x*x*x is equal to 2024"? And why might this specific number, 2024, be interesting in this context? We'll explore the steps involved in figuring out 'x', look at why this kind of math matters, and perhaps even touch on some broader ideas about how numbers help us make sense of the world around us. It's a pretty neat topic, you know, especially when you start to see the connections.
Table of Contents
- Understanding the Cube Concept
- How to Solve for 'x'
- Why 2024 Matters in This Equation
- Real-World Glimpses of Cubic Relationships
- Frequently Asked Questions About Cubic Equations
- The Beauty of Numerical Puzzles
Understanding the Cube Concept
When you see "x*x*x," what we're really talking about is 'x' raised to the power of three, or 'x cubed'. This is a fundamental operation in mathematics, a bit like addition or multiplication, but it involves repeating the multiplication three times. For instance, if you have 2*2*2, that gives you 8. Or, if you have 5*5*5, that comes out to 125. This idea of cubing a number is pretty straightforward, actually, and it's something we encounter in many different areas, from simple arithmetic to more advanced geometry.
The term "cube" itself comes from geometry, as you might guess. Imagine a perfect three-dimensional box where all sides are exactly the same length. If 'x' represents the length of one of those sides, then the volume of that box would be x multiplied by x multiplied by x, or x cubed. So, when we say "x*x*x is equal to 2024," we're essentially asking: "What number, when used as the side length of a perfect cube, would give that cube a volume of 2024 cubic units?" It's a rather neat way to visualize the problem, I think.
This concept of cubing is quite distinct from just adding numbers together, like when we see "x+x equals 2x" or "x+x+x equals 3x" in basic algebra. Those are about combining equal things, you know? Cubing, on the other hand, is about scaling up in a very specific, three-dimensional way. It's a core idea that shows up in various mathematical problems, much like the kinds of questions you might find in previous year questions with solutions of mathematics from JEE Main, where understanding such basic operations is pretty important.
How to Solve for 'x'
Now, let's get to the heart of the matter: how do you actually figure out what 'x' is when "x*x*x is equal to 2024"? This involves finding the inverse operation of cubing, which is called taking the cube root. Just as division undoes multiplication, and subtraction undoes addition, the cube root undoes cubing. It's a pretty clever way to work backwards and find the original number.
The Mathematical Approach
To solve x*x*x = 2024, we write it mathematically as x³ = 2024. To isolate 'x', we take the cube root of both sides. This is usually represented with a special symbol, a radical sign with a small '3' above it, like this: ∛. So, the equation becomes x = ∛2024. Finding the exact value of this can be a bit tricky without a calculator, but the process is clear. It's similar to how you might approach a function problem like f(x) = |x-1|, g(x) = [x], and h(x) = f(x)g(x), where you need to apply specific operations to find a solution, you know?
For most numbers that aren't perfect cubes (meaning they aren't the result of an integer multiplied by itself three times), the cube root will be a decimal number, often one that goes on for quite a while. 2024 is not a perfect cube. For example, 12 cubed (12*12*12) is 1728, and 13 cubed (13*13*13) is 2197. So, we know right away that 'x' must be somewhere between 12 and 13. This kind of estimation is a pretty good first step, actually, helping us get a feel for the number.
To get a precise value, you would typically use a calculator or a computer program. When you input ∛2024, the result you get is approximately 12.646. So, when you multiply 12.646 by itself three times (12.646 * 12.646 * 12.646), you get a number very, very close to 2024. It's a pretty neat demonstration of how precise mathematics can be, even with numbers that aren't perfectly clean.
Approximating the Solution
Even without a fancy calculator, you can get a good estimate. Since 2024 is closer to 2197 (13³) than it is to 1728 (12³), you'd expect 'x' to be closer to 13 than to 12. You could try numbers like 12.5 or 12.6 and cube them to see how close you get. For instance, 12.5 * 12.5 * 12.5 equals 1953.125, which is a bit too low. Trying 12.7 * 12.7 * 12.7 gives you 2048.383, which is a little too high. This iterative process, you know, trying and refining, is a very practical way to approach such problems, especially in a pinch.
This method of approximation is pretty useful, especially for understanding the concept without needing immediate exact figures. It shows how you can narrow down the possibilities and get a feel for the number. It's a skill that's often helpful in various problem-solving situations, not just math. Sometimes, just getting close is good enough to move forward, particularly when you're trying to troubleshoot something, like figuring out why you can't receive a verification code on TG, where you check network connections and other steps to narrow down the issue.
The ability to estimate and work with approximations is, in some respects, a sign of a deeper understanding. It shows you're not just relying on a tool, but you actually grasp the numerical relationships involved. It's a bit like knowing that different flight cabin classes, from First Class (F) to Economy (Y) with its various sub-classes like X and E, represent a range of options; you don't need to know the exact price of every single one to understand the general hierarchy and what they offer.
Why 2024 Matters in This Equation
The number 2024, in this context, is rather significant because it's the current year for many of us. This makes the equation "x*x*x is equal to 2024" feel a bit more timely and relevant. It connects a mathematical curiosity directly to our present moment, you know? It's not just some random number pulled out of thin air; it's the year we're experiencing, making the problem feel a little more personal, perhaps.
As we've seen, 2024 is not a perfect cube. This means that 'x' isn't a neat whole number. This fact, in itself, is interesting. It highlights that not every mathematical problem will yield a clean, integer solution. Many real-world measurements and calculations involve numbers that aren't perfectly divisible or whole, and mathematics provides us with the tools to work with these less-than-perfect figures. It's a pretty good example of how math often reflects the messy, yet precise, nature of the world.
The year 2024 also serves as a reminder that mathematics is constantly relevant, even in seemingly simple ways. Just as we might see new updates and improvements in technology, like the latest RTX 5050 graphics cards being benchmarked for 1080P/2K/4K resolution gaming, mathematics continues to be the bedrock upon which many of these advancements are built. The principles of cubing and cube roots, while ancient, are still pretty fundamental to understanding volumes, scaling, and various other scientific and engineering applications. It's a bit like how a hero, or "yingxiong," in a trailer might face a challenge that requires a deep understanding of their abilities; solving this equation requires understanding the 'abilities' of numbers.
Real-World Glimpses of Cubic Relationships
While "x*x*x is equal to 2024" might seem like a purely academic exercise, the concept of cubing and cube roots pops up in many practical areas. Anywhere you're dealing with three-dimensional space, you're likely to encounter cubic relationships. For example, if you're designing a water tank, a shipping container, or even just calculating the amount of dirt needed to fill a hole, you'll be working with volume, which is often measured in cubic units. So, understanding how to find a side length from a given volume is a very practical skill, actually.
Consider engineering and architecture. Architects and engineers regularly calculate volumes of materials needed for construction. If they know the desired volume of a cubic structure, they'd need to find its side length using the cube root. Similarly, in physics, certain formulas for density or pressure might involve cubic terms. It's a pretty common occurrence, you know, where these mathematical operations become truly useful tools. It's not just about theoretical problems; it's about building and designing things in the real world.
Even in fields like computer graphics, which often deal with resolutions like 1080P, 2K, or 4K, the underlying principles of scaling and three-dimensional rendering rely on mathematical concepts that include cubic functions. While a specific problem like "x*x*x = 2024" might not directly appear on a screen, the mathematical ideas behind it are consistently used to create the visuals we see. It's a bit like the complex mathematical functions, perhaps with "math processing error" notations, that underpin advanced calculations in areas like differential equations or definite integration, which are critical for various scientific models.
Frequently Asked Questions About Cubic Equations
People often have questions when they first encounter equations like x³ = 2024. Here are a few common ones that might come to mind, much like the "People Also Ask" sections you see on search engines, or the kinds of questions people post on a community platform like Zhihu, seeking clear, helpful answers.
What is a "perfect cube"?
A perfect cube is any integer that results from multiplying another integer by itself three times. For example, 8 is a perfect cube because 2*2*2 equals 8. Similarly, 27 is a perfect cube because 3*3*3 equals 27. When you take the cube root of a perfect cube, you always get a whole number. 2024, as we found out, is not a perfect cube, which is why its cube root is a decimal, you know?
Are there negative solutions for x*x*x = 2024?
For an equation like x³ = 2024, there is only one real number solution, and it's positive. This is because a negative number multiplied by itself three times (a negative times a negative times a negative) will always result in a negative number. For instance, (-2)*(-2)*(-2) equals -8. Since 2024 is a positive number, 'x' must also be positive. There are, however, complex (or imaginary) solutions in higher mathematics, but for most everyday purposes, we focus on the real solution. It's a pretty important distinction, actually, for understanding the full scope of such problems.
How is solving x*x*x = 2024 different from x*x = 2024?
The difference is pretty big, actually! When you have x*x = 2024 (or x² = 2024), you're looking for the square root of 2024. This means finding a number that, when multiplied by itself *twice*, gives you 2024. The solution for x² = 2024 would be approximately 44.989, and there would be both a positive and a negative solution (e.g., 44.989 and -44.989), because a negative number multiplied by a negative number gives a positive result. So, the number of times 'x' is multiplied makes a very significant difference in how you solve the problem and what kind of answer you get, you know?
The Beauty of Numerical Puzzles
Equations like "x*x*x is equal to 2024" are more than just abstract problems; they are, in a way, small puzzles that invite us to think critically and apply logical steps. They highlight the precision and consistency of mathematics, where every operation has a clear inverse, and every number has a specific place. It's a pretty fascinating aspect of how numbers work, I think.
Whether you're someone who loves to solve complex mathematical challenges, perhaps like those found in previous year questions with solutions of mathematics from JEE Main, or just someone who enjoys a good mental exercise, understanding these basic principles is pretty rewarding. It helps build a foundation for more complex ideas, and it shows that even a seemingly simple question can lead to a deeper appreciation of the numerical world around us. So, the next time you see a mathematical expression, remember it's an invitation to explore and discover something new. Learn more about mathematical concepts on our site, and you can also link to this page for a deeper dive into cube roots.
Just as you might troubleshoot a problem with Origin drawing software where the coordinate axes have a persistent horizontal line, solving a cubic equation involves a systematic approach. You check the knowns, apply the right operations, and work towards the unknown. It's a rather satisfying process, you know, bringing clarity to what might initially seem like a jumble of numbers. And that, in a way, is the true magic of mathematics.

x*x*x is Equal to | x*x*x equal to ? | Knowledge Glow

A Nice Math Equation • X=? - YouTube
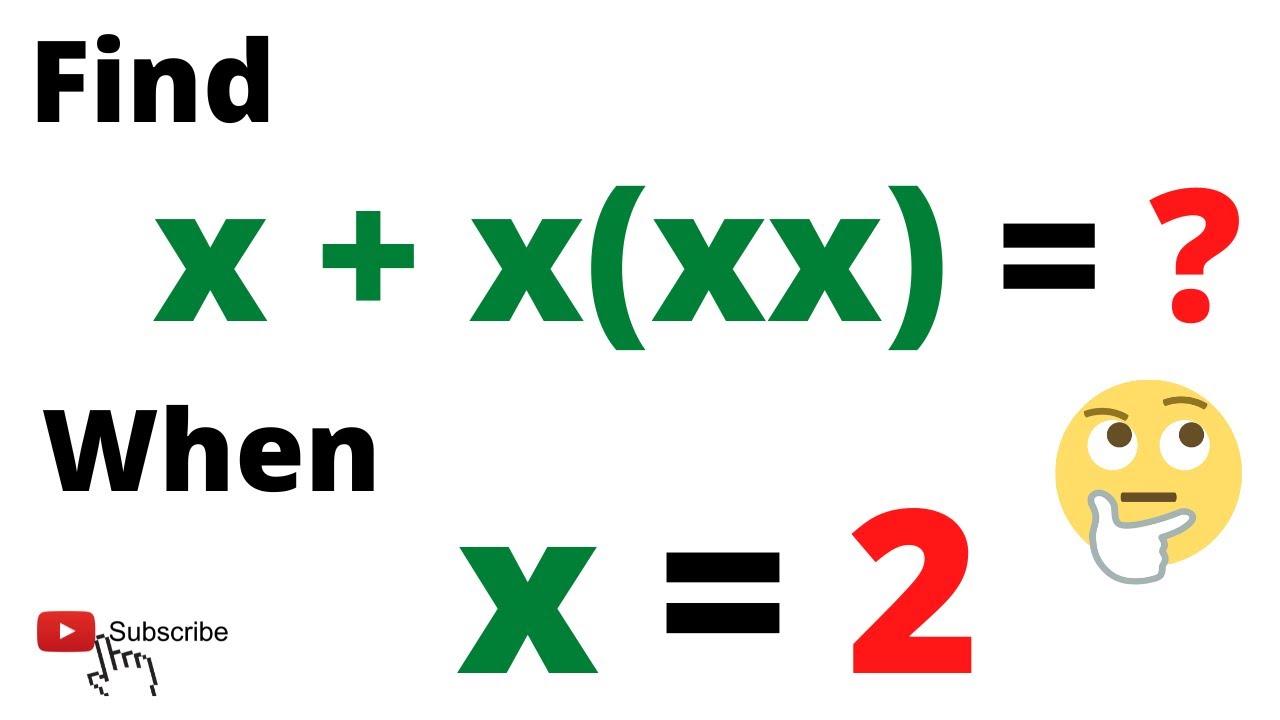
The value of x + x(xx) when x = 2 is: | Find the Answer in Seconds